The initial kinetic energy of the ball is
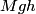 . The final kinetic energy is . The final kinetic energy is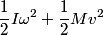 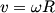 and for a hoop and for a hoop 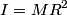 , so the final kinetic energy is , so the final kinetic energy is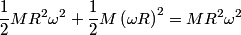 So, 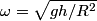 The angular momentum about the center of mass is 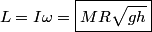 Therefore, answer (A) is correct. |
The initial kinetic energy of the ball is
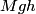 . The final kinetic energy is . The final kinetic energy is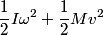 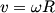 and for a hoop and for a hoop 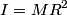 , so the final kinetic energy is , so the final kinetic energy is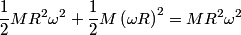 So, 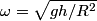 The angular momentum about the center of mass is 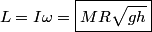 Therefore, answer (A) is correct. |